Eliminasi Gauss
Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Metode Eliminasi Gauss adalah salah satu cara yang paling awal dan banyak digunakan dalam penyelesaian sistem persamaan linier. Cara ini ditemukan oleh Carl Friedrich Gauss. Prosedur penyelesaian dari metode ini adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Ciri-ciri Eliminasi Gauss
rumus baris 2 kolom 1 menjadi 0 yaitu kalikan -2 dengan baris 1 kemudian ditambahkan baris 2 (-2.b1+b2)
rumus baris 3 kolom 1 menjadi 0 yaitu kalikan -3 dengan baris 1 kemudian ditambahkan baris 2 (-3.b1+b3)

rumus baris 3 kolom 3 menjadi 1 yaitu kalikan -1 dengan baris 3 (-1.b3)
Eliminasi Gauss Jordan
Eliminasi Gauss Jordan adalah Salah satu metode yang dapat digunakan untuk menyelesaikan sistem persamaan linier adalah metode eliminasi Gauss-Jordan. Metode ini diberi nama Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Wilhelm Jordan. Metode ini sebenarnya adalah modifikasi dari metode eliminasi Gauss, yang dijelaskan oleh Jordan di tahun 1887. Metode Gauss-Jordan ini menghasilkan matriks dengan bentuk baris eselon yang tereduksi(reduced row echelon form), sementara eliminasi Gauss hanya menghasilkan matriks sampai padabentuk baris eselon (row echelon form). Selain untuk menyelesaikan sistem persamaan linier, metode eliminasi Gauss-Jordan ini dapat menyelesaikan matriks. Metode Eliminasi Gauss : metode yang dikembangkan dari metode eliminasi, yaitu menghilangkanatau mengurangi jumlah variable sehingga dapat diperoleh nilai dari suatu variable yang bebas. Eliminasi Gauss Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris tereduksi. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris tereduksi, maka langsung dapat ditentukan nilai dari variabel variabelnya tanpa substitusi balik.
Metode ini digunakan untuk mencari invers dari sebuah matriks.
Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah
Mengubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. merupakan variasi dari eliminasi gauss dengan kebutuhan dapat menyelesaikan matriks invers.
Contoh Penyelesaiannya dalam sebuah matriks ber ordo 3x3
rumus baris 2 kolom 1 menjadi 0 yaitu kalikan -2 dengan baris 1 kemudian ditambahkan baris 2 (-2.b1+b2)
rumus baris 3 kolom 1 menjadi 0 yaitu kalikan -3 dengan baris 1 kemudian ditambahkan baris 2 (-3.b1+b3)

rumus baris 3 kolom 3 menjadi 1 yaitu kalikan -1 dengan baris 3 kolom 3 (-1.b33)
rumus baris 2 kolom 3 menjadi 0 yaitu tambahkan -1 dengan baris 2 kolom 3 (-1+b23)
rumus baris 1 kolom 3 menjadi 0 yaitu tambahkan -3 dengan baris 1 kolom 3 (-3+b13)
rumus baris 1 kolom 2 menjadi 0 yaitu tambahkan -2 dengan baris 1 kolom 2 (-2+b12)
.
Metode Sarrus
Determinan suatu matriks dapat dilakukan dengan berbagai metode, salah satunya yaitu dengan metode Sarrus. Metode Sarrus adalah salah satu cara untuk mencari suatu determinan matriks yang dapat digunakan untuk mencari determinan matriks berordo sampai dengan 3.
Contoh Penggunann Metode Sarrus :
Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Metode Eliminasi Gauss adalah salah satu cara yang paling awal dan banyak digunakan dalam penyelesaian sistem persamaan linier. Cara ini ditemukan oleh Carl Friedrich Gauss. Prosedur penyelesaian dari metode ini adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Ciri-ciri Eliminasi Gauss
- Jika suatu baris tidak semua nol, maka bilangan pertama yang tidak nol ada 1(1 utama).
- Baris nol terletak paling bawah.
- 1 utama baris berikutnya berada dikanan 1 utama baris diatasnya.
- Dibawah 1 utama harus nol.

rumus baris 2 kolom 1 menjadi 0 yaitu kalikan -2 dengan baris 1 kemudian ditambahkan baris 2 (-2.b1+b2)
rumus baris 3 kolom 1 menjadi 0 yaitu kalikan -3 dengan baris 1 kemudian ditambahkan baris 2 (-3.b1+b3)

rumus baris 3 kolom 3 menjadi 1 yaitu kalikan -1 dengan baris 3 (-1.b3)
Eliminasi Gauss Jordan
Eliminasi Gauss Jordan adalah Salah satu metode yang dapat digunakan untuk menyelesaikan sistem persamaan linier adalah metode eliminasi Gauss-Jordan. Metode ini diberi nama Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Wilhelm Jordan. Metode ini sebenarnya adalah modifikasi dari metode eliminasi Gauss, yang dijelaskan oleh Jordan di tahun 1887. Metode Gauss-Jordan ini menghasilkan matriks dengan bentuk baris eselon yang tereduksi(reduced row echelon form), sementara eliminasi Gauss hanya menghasilkan matriks sampai padabentuk baris eselon (row echelon form). Selain untuk menyelesaikan sistem persamaan linier, metode eliminasi Gauss-Jordan ini dapat menyelesaikan matriks. Metode Eliminasi Gauss : metode yang dikembangkan dari metode eliminasi, yaitu menghilangkanatau mengurangi jumlah variable sehingga dapat diperoleh nilai dari suatu variable yang bebas. Eliminasi Gauss Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris tereduksi. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris tereduksi, maka langsung dapat ditentukan nilai dari variabel variabelnya tanpa substitusi balik.
Metode ini digunakan untuk mencari invers dari sebuah matriks.
Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah
- Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.
- Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks A menjadi dalam bentuk baris eselon yang tereduksi.

Mengubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. merupakan variasi dari eliminasi gauss dengan kebutuhan dapat menyelesaikan matriks invers.
Contoh Penyelesaiannya dalam sebuah matriks ber ordo 3x3
rumus baris 2 kolom 1 menjadi 0 yaitu kalikan -2 dengan baris 1 kemudian ditambahkan baris 2 (-2.b1+b2)
rumus baris 3 kolom 1 menjadi 0 yaitu kalikan -3 dengan baris 1 kemudian ditambahkan baris 2 (-3.b1+b3)

rumus baris 3 kolom 3 menjadi 1 yaitu kalikan -1 dengan baris 3 kolom 3 (-1.b33)
rumus baris 2 kolom 3 menjadi 0 yaitu tambahkan -1 dengan baris 2 kolom 3 (-1+b23)
rumus baris 1 kolom 3 menjadi 0 yaitu tambahkan -3 dengan baris 1 kolom 3 (-3+b13)
rumus baris 1 kolom 2 menjadi 0 yaitu tambahkan -2 dengan baris 1 kolom 2 (-2+b12)
.
Metode Sarrus
Determinan suatu matriks dapat dilakukan dengan berbagai metode, salah satunya yaitu dengan metode Sarrus. Metode Sarrus adalah salah satu cara untuk mencari suatu determinan matriks yang dapat digunakan untuk mencari determinan matriks berordo sampai dengan 3.
Contoh Penggunann Metode Sarrus :
1. tentukan determinan matriks berikut ini !
maka determinan dari matrik A, yaitu :
det A = 2.6.4 + (-1).3.1 + (-5).(-4).5 - (-5).6.1 - 2.3.5 - (-1).(-4).4
= 48+(-3)+100-(-30)-(30)-16
= 129
Cramer
Cramer adalah rumus yang dapat digunakan untuk menyelesaikan sistem persamaan linear. Metode ini menggunakan determinan suatu matriks dan matriks lain yang diperoleh dengan mengganti salah satu kolom dengan vektor yang terdiri dari angka disebelah kanan persamaannya.
Cara Aturan Cramer :
1. Rubah bentuk SPL menjadi persamaan matriks.
2. Tentukan masing-masing nilai determinan dari matriks A,A1,A2 dan A3
yaitu |A|,|A1|A2|,|A3|
A1= Matriks A yang kolom ke 1 nya diganti dengan b.
A2= Matriks A yang kolom ke 2 nya diganti dengan b.
A3= Matriks A yang kolom ke 3 nya diganti dengan b.
3. Tentukan nilai 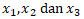
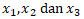
Penyelesaian :
Diketahui
Tentukan masing-masing nilai determinan dari matriks |A|,|A1|,|A2|,|A3|
|A| = 2.6.4 + (-1).3.1 + (-5).(-4).5 - (-5).6.1 - 2.3.5 - (-1).(-4).4
= 48+(-3)+100-(-30)-(30)-16
= 129
|A1| = (-30).6.4 + (-1).3.46 + (-5).34.5 - (-5).6.46 - (-30).3.5 - (-1).34.4
= (-720)+(-138)+(-850)-(-1380)-(-450)-(-136)
= 258
|A2| = 2.34.4 + (-30).3.1 + (-5).(-4).46 - (-5).34.1 - 2.3.46 - (-30).(-4).4
= 272+(-90)+920-(-170)-276-480
= 516
|A3| = 2.6.46 + (-1).34.1 + (-30).(-4).5 - (-30).6.1 - 2.34.5 - (-1).(-4).46
= 552+(-34)+600-(-180)-340-184
= 774
Tentukan nilai 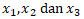
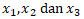
Semoga dapat bermanfaat ya guys.
.




















